Stack In C++ Stl

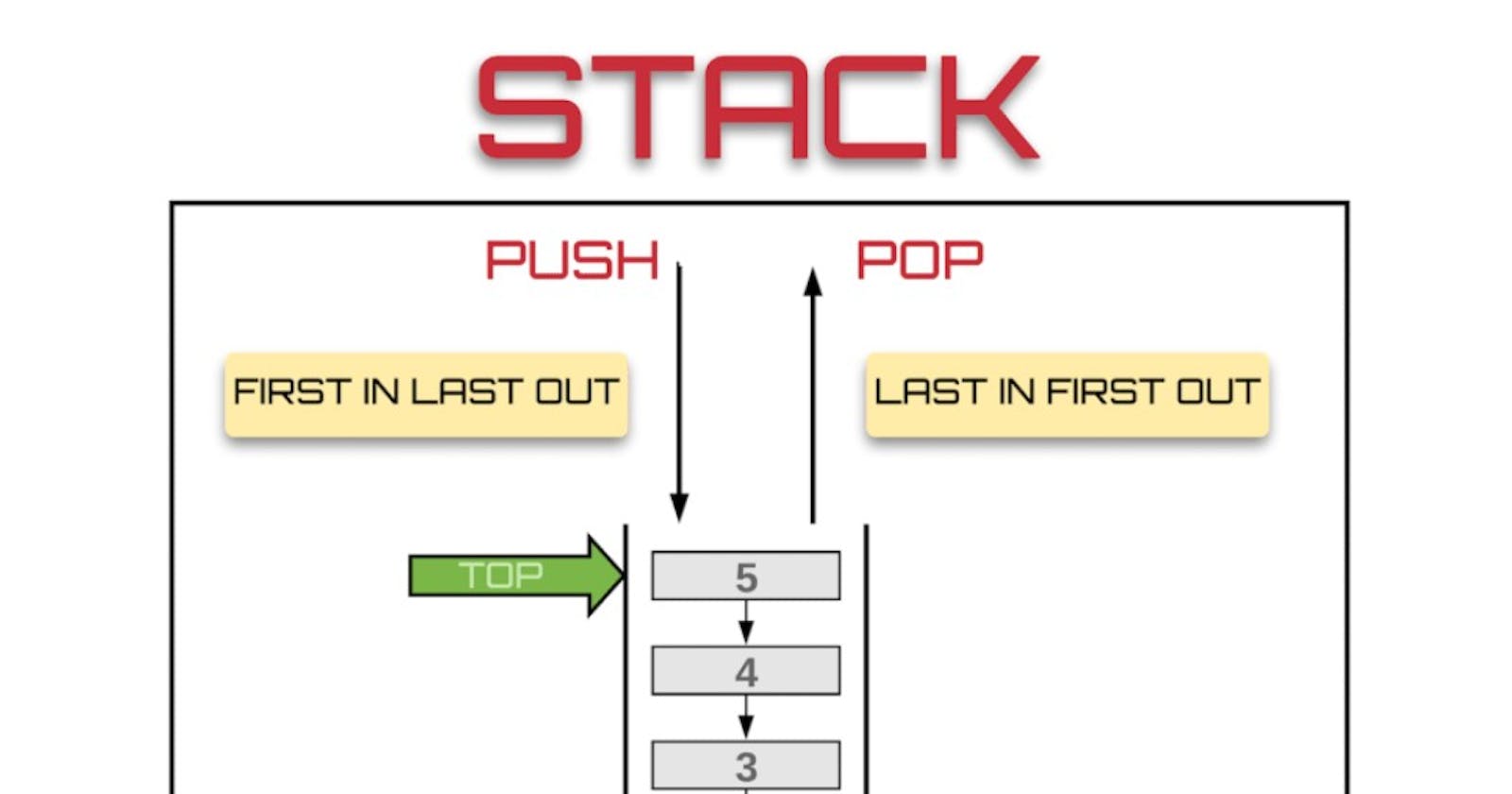
DESCRIPTION

• A container that follows the Last-In-First-Out (LIFO) principle, where the last element added is the first one to be removed.

• Provides a simple and efficient interface for basic stack operations.

• Suitable for scenarios where elements need to be added and removed from one end only.

ALL THE POSSIBLE WAYS TO DECLARE, INITIALIZE AND PRINTING STACK:

#include <iostream>
#include <stack>

using namespace std;

int main() {
    // Declaration of an empty stack of integers
    stack<int> myStack;

    // Initializing stack using push
    myStack.push(10);
    myStack.push(20);
    myStack.push(30);

    // Printing stack using while loop and top
    cout << "Stack Contents (top to bottom): ";
    while (!myStack.empty()) {
        cout << myStack.top() << " ";
        myStack.pop();
    }
    cout << endl;

    return 0;
}

OUTPUT:

Stack Contents (top to bottom): 30 20 10

MEMBER FUNCTIONS:

1. Empty:

   • Works: Checking whether the stack is empty.

   • Syntax: empty()

   • Example:

       stack<int> myStack;
       bool isEmpty = myStack.empty();
     

2. Size:

   • Works: Getting the number of elements in the stack.

   • Syntax: size()

   • Example:

       stack<int> myStack;
       size_t stackSize = myStack.size();
     

3. Top:

   • Works: Getting a reference to the top element in the stack.

   • Syntax: top()

   • Example:

       stack<int> myStack;
       myStack.push(42);
       int topElement = myStack.top();
     

     CODE:

       #include <iostream>
       #include <stack>
     
       int main() {
           // Empty
           std::stack<int> emptyStack;
           bool isEmpty = emptyStack.empty();
           std::cout << "Is Empty: " << (isEmpty ? "Yes" : "No") << std::endl;
     
           // Size
           std::stack<int> sizeStack = {3, 7, 2, 8, 5};
           size_t stackSize = sizeStack.size();
           std::cout << "Stack Size: " << stackSize << std::endl;
     
           // Top
           std::stack<int> topStack;
           topStack.push(42);
           int topElement = topStack.top();
           std::cout << "Top Element: " << topElement << std::endl;
     
           return 0;
       }
     

     OUTPUT:

       Is Empty: Yes
       Stack Size: 5
       Top Element: 42
     

MODIFIERS:

1. Push:

   • Works: Adding an element to the top of the stack.

   • Syntax: push(const T& val)

   • Example:

       stack<int> myStack;
       myStack.push(42);
     

2. Pop:

• Works: Removing the top element from the stack.

• Syntax: pop()

• Example:

    stack<int> myStack;
    myStack.push(42);
    myStack.pop();
  

  CODE

    #include <iostream>
    #include <stack>
  
    int main() {
        // Push
        std::stack<int> pushStack;
        pushStack.push(42);
        std::cout << "Element pushed onto the stack." << std::endl;
  
        // Pop
        std::stack<int> popStack;
        popStack.push(42);
        popStack.pop();
        std::cout << "Top element popped from the stack." << std::endl;
  
        return 0;
    }
  

  OUTPUT:

    Element pushed onto the stack.
    Top element popped from the stack.
  

ALGORITHMS DIRECTLY APPLICABLE TO QUEUES:

1. Max Element:

   • Works: Finds the largest element in a stack.

   • Syntax: Iterate through the stack and keep track of the maximum element.

   • Example:

       stack<int> myStack = {3, 7, 2, 8, 5};
       int maxElement = INT_MIN;
     
       while (!myStack.empty()) {
           maxElement = max(maxElement, myStack.top());
           myStack.pop();
       }
     

2. Min Element:

   • Works: Finds the smallest element in a stack.

   • Syntax: Iterate through the stack and keep track of the minimum element.

   • Example:

       stack<int> myStack = {3, 7, 2, 8, 5};
       int minElement = INT_MAX;
     
       while (!myStack.empty()) {
           minElement = min(minElement, myStack.top());
           myStack.pop();
       }
     

3. Accumulate:

   • Works: Accumulates the result of an operation on a stack.

   • Syntax: Iterate through the stack and sum the elements.

   • Example:

       stack<int> myStack = {3, 7, 2, 8, 5};
       int sum = 0;
     
       while (!myStack.empty()) {
           sum += myStack.top();
           myStack.pop();
       }
     

CODE:

    #include <iostream>
    #include <stack>
    #include <climits>

    int main() {
        // Max Element
        std::stack<int> maxStack = {3, 7, 2, 8, 5};
        int maxElement = INT_MIN;

        while (!maxStack.empty()) {
            maxElement = std::max(maxElement, maxStack.top());
            maxStack.pop();
        }

        std::cout << "Max Element: " << maxElement << std::endl;

        // Min Element
        std::stack<int> minStack = {3, 7, 2, 8, 5};
        int minElement = INT_MAX;

        while (!minStack.empty()) {
            minElement = std::min(minElement, minStack.top());
            minStack.pop();
        }

        std::cout << "Min Element: " << minElement << std::endl;

        // Accumulate
        std::stack<int> accumulateStack = {3, 7, 2, 8, 5};
        int sum = 0;

        while (!accumulateStack.empty()) {
            sum += accumulateStack.top();
            accumulateStack.pop();
        }

        std::cout << "Sum of Elements: " << sum << std::endl;

        return 0;
    }

OUTPUT:

    Max Element: 8
    Min Element: 2
    Sum of Elements: 25

N.B: ALGORITHMS NOT DIRECTLY APPLICABLE TO QUEUES:

• Binary Search with Stacks:

  • Reason: Binary search relies on dividing the data in half, which requires random access to efficiently access the middle element. Stacks provide access only to the top element, making it challenging to divide the stack in half without additional data structures.

• Equal Range with Stacks:

  • Reason: Similar to binary search, finding a range efficiently requires random access. Stacks only provide access to the top element, making it less efficient to locate the first and last occurrences of a value.

• Inplace Merge with Stacks:

  • Reason: Inplace merge involves rearranging elements within the same container. Stacks, with their limited access to only the top element, make it challenging to perform efficient in-place merging.

• Lower Bound and Upper Bound with Stacks:

  • Reason: Efficiently finding the lower and upper bounds involves traversing elements in a sorted order. Stacks provide access only to the top element, making sequential traversal less efficient.

• Make Heap and Sort Heap with Stacks:

  • Reason: Building and sorting a heap efficiently require random access to elements. Stacks, with their limited access to only the top element, make it challenging to perform these operations efficiently.

• Merge with Stacks:

  • Reason: Merging two sorted ranges efficiently requires accessing elements from both ranges simultaneously. Stacks provide access only to the top element, making simultaneous access difficult.

• Partition with Stacks:

  • Reason: Partitioning involves rearranging elements based on a condition, and efficient partitioning often requires random access. Stacks provide access only to the top element, making it challenging to perform efficient partitioning.

• Sort and Stable Sort with Stacks:

  • Reason: Sorting involves rearranging elements efficiently, which is challenging with stacks due to their limited access to only the top element. Stable sorting, in particular, requires preserving the order of equal elements, which is harder to achieve with stacks.

  • CONGRATULATIONS..! NOW YOU ARE THE MASTER OF STACK CONTAINER.