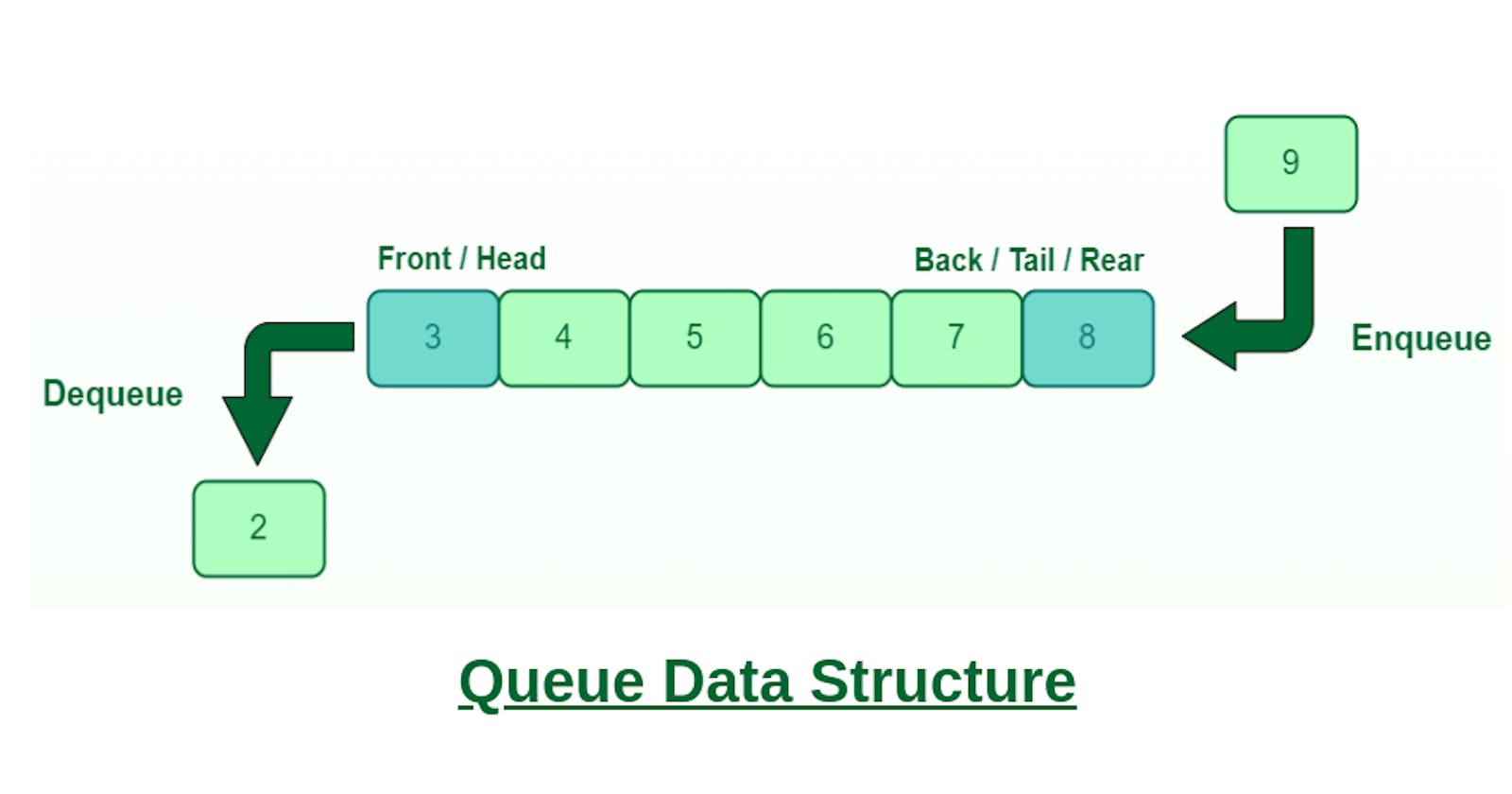
DESCRIPTION
A container that follows the First-In-First-Out (FIFO) principle, where the first element added is the first one to be removed.
Provides a simple and efficient interface for basic queue operations.
Suitable for scenarios where elements need to be added at one end (rear/enqueue) and removed from the other end (front/dequeue).
ALL THE POSSIBLE WAYS TO DECLARE, INITIALIZE AND PRINTING STACK:
#include <iostream>
#include <queue>
using namespace std;
int main() {
// Declaration of an empty queue of integers
queue<int> myQueue;
// Initializing queue using push
myQueue.push(10);
myQueue.push(20);
myQueue.push(30);
// Printing queue using while loop and front
cout << "Queue Contents (front to back): ";
while (!myQueue.empty()) {
cout << myQueue.front() << " ";
myQueue.pop();
}
cout << endl;
return 0;
}
OUTPUT:
Queue Contents (front to back): 10 20 30
MEMBER FUNCTIONS:
Empty:
Works: Checking whether the queue is empty.
Syntax:
empty()Example:
queue<int> myQueue; bool isEmpty = myQueue.empty();
Size:
Works: Getting the number of elements in the queue.
Syntax:
size()Example:
queue<int> myQueue; size_t queueSize = myQueue.size();
Front:
Works: Getting a reference to the front element in the queue.
Syntax:
front()Example:
queue<int> myQueue; myQueue.push(42); int frontElement = myQueue.front();
Back:
Works: Getting a reference to the back element in the queue.
Syntax:
back()
Example:
queue<int> myQueue;
myQueue.push(42);
int backElement = myQueue.back();
CODE:
#include <iostream>
#include <queue>
int main() {
// Declare a queue
std::queue<int> myQueue;
// Check if the queue is empty
if (myQueue.empty()) {
std::cout << "Queue is empty." << std::endl;
} else {
std::cout << "Queue is not empty." << std::endl;
}
// Add elements to the queue
myQueue.push(3);
myQueue.push(1);
myQueue.push(4);
myQueue.push(1);
myQueue.push(5);
myQueue.push(9);
// Get the number of elements in the queue
std::cout << "Number of elements in the queue: " << myQueue.size() << std::endl;
// Access the front element
std::cout << "Front element of the queue: " << myQueue.front() << std::endl;
// Access the back element
std::cout << "Back element of the queue: " << myQueue.back() << std::endl;
// Display and remove elements from the front of the queue
std::cout << "Elements in the queue: ";
while (!myQueue.empty()) {
std::cout << myQueue.front() << " ";
myQueue.pop(); // Remove the front element
}
std::cout << std::endl;
return 0;
}
OUTPUT:
Queue is empty.
Number of elements in the queue: 6
Front element of the queue: 3
Back element of the queue: 9
Elements in the queue: 3 1 4 1 5 9
MODIFIERS:
Certainly! Here's how you can use these functions with queues:
Push:
Works: Adding an element to the back of the queue.
Syntax:
push(const T& val)Example:
queue<int> myQueue; myQueue.push(42);
Pop:
Works: Removing the front element from the queue.
Syntax:
pop()
Example:
queue<int> myQueue;
myQueue.push(42);
myQueue.pop();
CODE:
CODE 👍
#include <iostream>
#include <queue>
using namespace std;
int main() {
// Declare a queue
queue<int> myQueue;
// Add elements to the back of the queue using push(const T& val)
myQueue.push(3);
myQueue.push(1);
myQueue.push(4);
// Display elements in the queue after push operations
cout << "Elements in the queue after push operations: ";
while (!myQueue.empty()) {
cout << myQueue.front() << " ";
myQueue.pop(); // Remove the front element
}
cout << endl;
// Add elements to the back of the queue using push(const T& val)
myQueue.push(5);
myQueue.push(9);
// Display elements in the queue after additional push operations
cout << "Elements in the queue after additional push operations: ";
while (!myQueue.empty()) {
cout << myQueue.front() << " ";
myQueue.pop(); // Remove the front element
}
cout << endl;
return 0;
}
OUTPUT:
Elements in the queue after push operations: 3 1 4
Elements in the queue after additional push operations: 5 9
ALGORITHM
ALGORITHMS DIRECTLY APPLICABLE TO QUEUES:
Max Element:
Works: Finds the largest element in a queue.
Syntax: Iterate through the queue and keep track of the maximum element.
Example:
queue<int> myQueue = {3, 7, 2, 8, 5}; int maxElement = INT_MIN; while (!myQueue.empty()) { maxElement = max(maxElement, myQueue.front()); myQueue.pop(); }
Min Element:
Works: Finds the smallest element in a queue.
Syntax: Iterate through the queue and keep track of the minimum element.
Example:
queue<int> myQueue = {3, 7, 2, 8, 5}; int minElement = INT_MAX; while (!myQueue.empty()) { minElement = min(minElement, myQueue.front()); myQueue.pop(); }
Accumulate:
Works: Accumulates the result of an operation on a queue.
Syntax: Iterate through the queue and sum the elements.
Example:
queue<int> myQueue = {3, 7, 2, 8, 5}; int sum = 0; while (!myQueue.empty()) { sum += myQueue.front(); myQueue.pop(); }CODE:
#include <iostream> #include <queue> #include <climits> int main() { // Max Element std::queue<int> maxQueue; maxQueue.push(3); maxQueue.push(7); maxQueue.push(2); maxQueue.push(8); maxQueue.push(5); int maxElement = INT_MIN; while (!maxQueue.empty()) { maxElement = std::max(maxElement, maxQueue.front()); maxQueue.pop(); } std::cout << "Max Element: " << maxElement << std::endl; // Min Element std::queue<int> minQueue; minQueue.push(3); minQueue.push(7); minQueue.push(2); minQueue.push(8); minQueue.push(5); int minElement = INT_MAX; while (!minQueue.empty()) { minElement = std::min(minElement, minQueue.front()); minQueue.pop(); } std::cout << "Min Element: " << minElement << std::endl; // Accumulate std::queue<int> accumulateQueue; accumulateQueue.push(3); accumulateQueue.push(7); accumulateQueue.push(2); accumulateQueue.push(8); accumulateQueue.push(5); int sum = 0; while (!accumulateQueue.empty()) { sum += accumulateQueue.front(); accumulateQueue.pop(); } std::cout << "Sum of Elements: " << sum << std::endl; return 0; }OUTPUT:
Max Element: 8 Min Element: 2 Sum of Elements: 25N.B: ALGORITHMS NOT DIRECTLY APPLICABLE TO QUEUES:
Binary Search:
Binary search relies on accessing elements at the middle of a sorted collection, which queues don't support efficiently.
Instead, for a binary search-like operation, you could iterate through the queue, checking if the target value is present.
equal_range():
Similar to binary search, equal_range() needs random access.
You could iterate through the queue and maintain a range of elements matching a given value.
inplace_merge():
In-place merging involves merging two sorted ranges without additional memory allocations, which is challenging with queues.
You might need to use additional data structures or consider a different approach based on your specific use case.
lower_bound() and upper_bound():
These algorithms require sorted sequences and random access.
For a queue, you would need to consider sorting it first or use alternative methods to find lower and upper bounds.
make_heap() and sort_heap():
These heap operations assume random access and efficient manipulation of elements.
For a queue, you might need to reconsider the use of a priority queue, which is a more suitable data structure for heap operations.
merge():
Merging two sorted ranges efficiently requires random access, making it challenging with queues.
Consider using other data structures or sorting the queue before merging.
partition():
Partitioning elements based on a condition efficiently involves moving elements around, which queues do not support well.
You might need to use other data structures or reconsider the need for partitioning in a queue contex.
CONGRATULATIONS ! NOW YOU ARE THE MASTER OF QUEUE CONTAINER.